Unveiling the Power of the Lambert Conformal Conic Projection: A Comprehensive Guide
Related Articles: Unveiling the Power of the Lambert Conformal Conic Projection: A Comprehensive Guide
Introduction
With enthusiasm, let’s navigate through the intriguing topic related to Unveiling the Power of the Lambert Conformal Conic Projection: A Comprehensive Guide. Let’s weave interesting information and offer fresh perspectives to the readers.
Table of Content
Unveiling the Power of the Lambert Conformal Conic Projection: A Comprehensive Guide
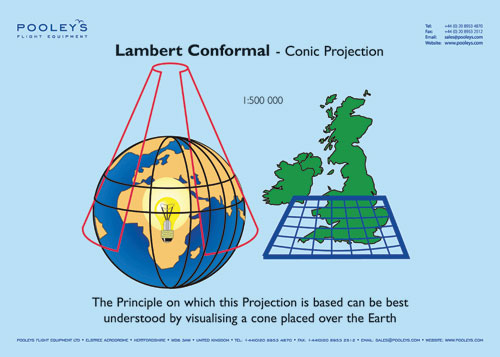
The world, in its vast and complex entirety, presents a significant challenge for cartographers. Representing the Earth’s three-dimensional surface on a flat map necessitates a transformation, introducing inevitable distortions. Enter the Lambert Conformal Conic Projection, a powerful tool that effectively balances these distortions, making it a cornerstone of mapmaking across various disciplines.
Understanding the Essence of the Lambert Conformal Conic Projection
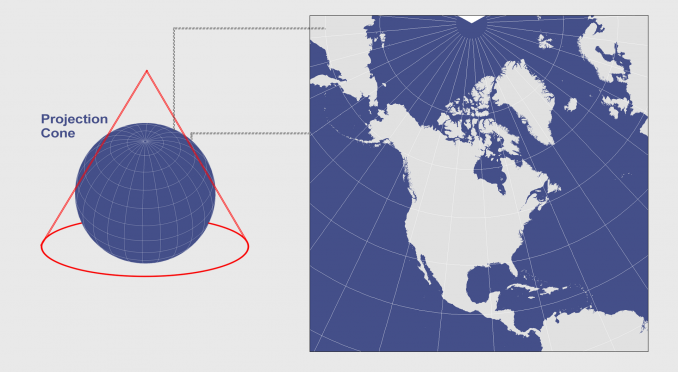
The Lambert Conformal Conic Projection, often referred to simply as the Lambert Projection, is a type of map projection that utilizes a cone to represent the Earth’s surface. This projection is categorized as a conformal projection, meaning it preserves angles and shapes locally, ensuring that relative sizes and directions are accurately depicted within a limited area.
The Mechanics of the Projection
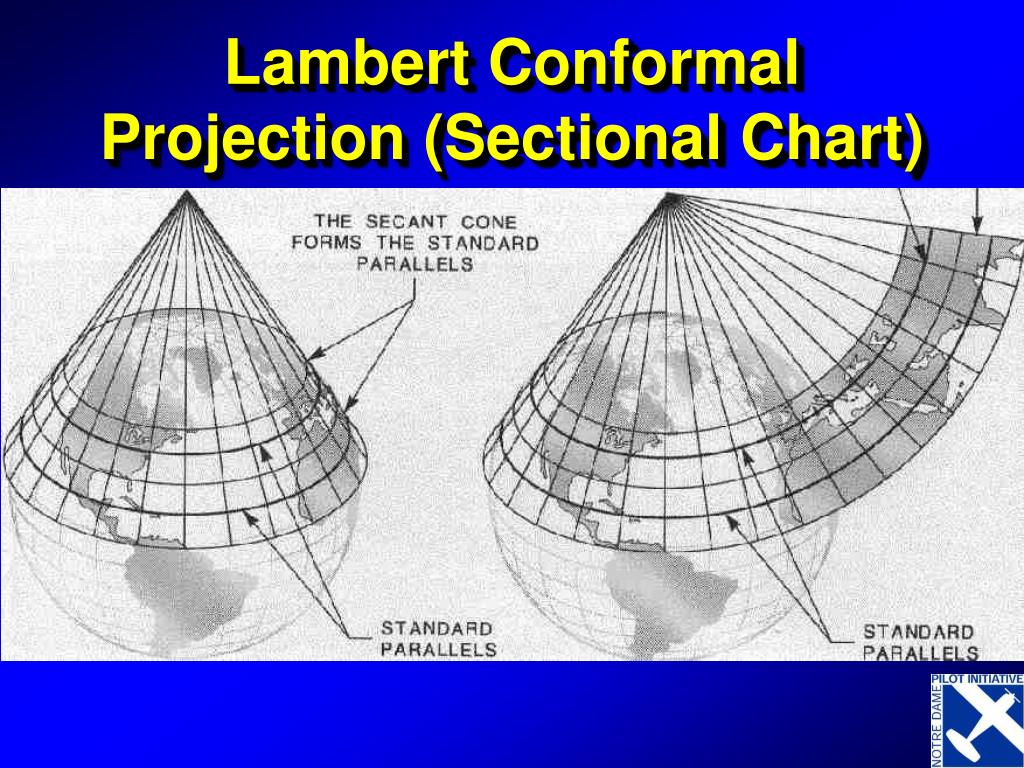
The projection process involves envisioning a cone intersecting the Earth at two standard parallels. The point of intersection between the cone and the Earth’s surface forms the standard parallels, which are crucial for defining the projection’s properties. The cone is then unrolled, creating a flat map. The region between the standard parallels experiences minimal distortion, making it ideal for mapping areas with significant longitudinal extent.
Key Features and Benefits of the Lambert Conformal Conic Projection:
- Preservation of Angles: This projection accurately depicts angles, making it suitable for applications requiring precise directional information.
- Minimal Distortion: The Lambert Projection minimizes distortion within the region between the standard parallels, ensuring accurate representation of shapes and relative sizes.
- Versatility: Its ability to accommodate a wide range of map scales and map extents makes it highly versatile for various applications.
- Ease of Use: The projection’s mathematical simplicity and well-defined properties facilitate ease of use and understanding.
Applications of the Lambert Conformal Conic Projection:
The Lambert Conformal Conic Projection finds wide-ranging applications across numerous disciplines, including:
- Cartography: It serves as a foundational projection for creating maps of countries, states, and regions, particularly those spanning significant longitudinal distances.
- Geography: It facilitates the analysis of geographic data, particularly in studies involving spatial relationships, land use, and resource management.
- Engineering: Its accuracy in representing angles and shapes is crucial for various engineering applications, including surveying, infrastructure planning, and construction.
- Navigation: The projection’s ability to depict accurate directions is vital for navigation purposes, especially in areas with significant longitudinal extent.
- Military Applications: The Lambert Conformal Conic Projection plays a significant role in military operations, including targeting, reconnaissance, and logistics.
Examples of Maps Using the Lambert Conformal Conic Projection:
- The United States Geological Survey (USGS) uses the Lambert Conformal Conic Projection for its topographic maps.
- The National Oceanic and Atmospheric Administration (NOAA) utilizes the Lambert Conformal Conic Projection for its nautical charts.
- Many state and regional maps employ the Lambert Conformal Conic Projection due to its suitability for mapping areas with significant longitudinal extent.
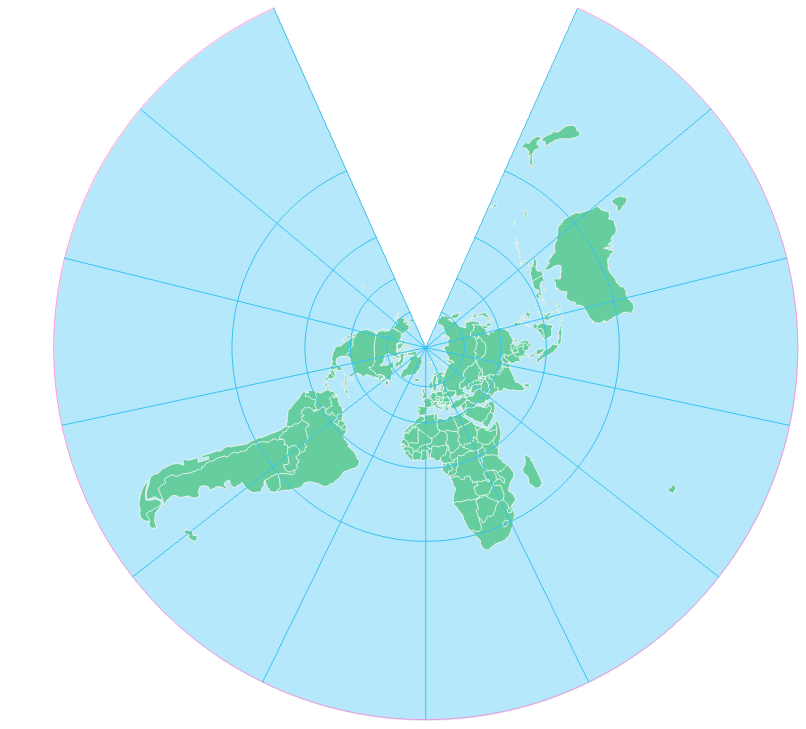
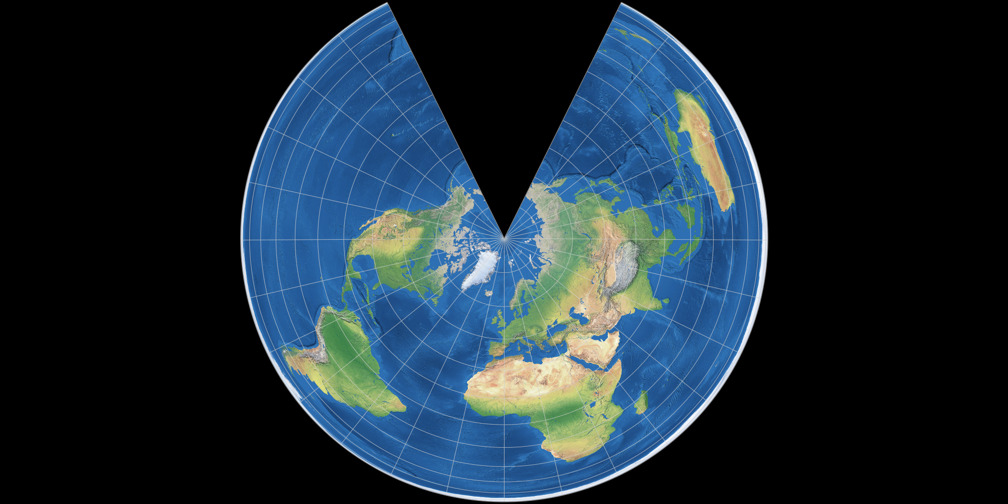
Understanding the Distortions Introduced by the Projection:
While the Lambert Conformal Conic Projection minimizes distortion within the region between the standard parallels, it is important to understand the distortions introduced beyond this zone.
- Area Distortion: Areas outside the standard parallels become increasingly distorted as distance from the standard parallels increases. This means that areas closer to the poles appear larger than they actually are.
- Shape Distortion: Shapes become increasingly elongated or compressed as distance from the standard parallels increases. This is particularly evident in areas near the edges of the map.
- Scale Distortion: The scale of the map varies depending on the location, with areas closer to the standard parallels having a more accurate scale.
Choosing the Right Standard Parallels:
The selection of standard parallels significantly impacts the projection’s characteristics and distortion patterns. Choosing appropriate standard parallels is crucial for minimizing distortion within the area of interest.
- For maps covering a large longitudinal extent, standard parallels should be chosen closer to the center of the mapped region. This minimizes area and shape distortion within the central region.
- For maps covering a smaller longitudinal extent, standard parallels can be chosen closer to the edges of the mapped region. This minimizes distortion in the areas closer to the edges of the map.
The Lambert Conformal Conic Projection: A Powerful Tool for Mapping the Earth’s Surface
The Lambert Conformal Conic Projection stands as a powerful tool for accurately representing the Earth’s surface on a flat map. Its ability to preserve angles and minimize distortion within a specific region makes it a preferred choice for various applications, including cartography, geography, engineering, and navigation.
Frequently Asked Questions (FAQs)
Q: What is the Lambert Conformal Conic Projection?
A: The Lambert Conformal Conic Projection is a map projection that uses a cone to represent the Earth’s surface. It is a conformal projection, meaning it preserves angles and shapes locally.
Q: What are the standard parallels in a Lambert Conformal Conic Projection?
A: Standard parallels are two specific lines of latitude where the cone intersects the Earth’s surface. They define the region of minimal distortion.
Q: What are the advantages of using the Lambert Conformal Conic Projection?
A: The Lambert Projection offers several advantages, including accurate angle representation, minimal distortion within the standard parallels, versatility, and ease of use.
Q: What are the limitations of the Lambert Conformal Conic Projection?
A: The Lambert Projection introduces distortion beyond the standard parallels, with areas further from the parallels experiencing greater distortion in area, shape, and scale.
Q: What are some applications of the Lambert Conformal Conic Projection?
A: The Lambert Projection finds applications in cartography, geography, engineering, navigation, and military operations.
Q: How do I choose the right standard parallels for a Lambert Conformal Conic Projection?
A: The choice of standard parallels depends on the extent and shape of the mapped region. Standard parallels should be chosen to minimize distortion within the area of interest.
Tips for Using the Lambert Conformal Conic Projection
- Understand the distortion patterns: Be aware of the distortions introduced by the Lambert Projection, particularly in areas outside the standard parallels.
- Choose appropriate standard parallels: Select standard parallels that minimize distortion within the area of interest.
- Use appropriate map scales: The choice of map scale influences the level of distortion.
- Consider alternative projections: If the Lambert Projection is not suitable for a particular application, explore other map projections that may be more appropriate.
Conclusion
The Lambert Conformal Conic Projection stands as a testament to the ingenuity of cartographers. Its ability to balance distortion and preserve angles within a specific region makes it a valuable tool for representing the Earth’s surface accurately. Understanding its strengths and limitations is crucial for selecting the most appropriate map projection for any given application. By harnessing the power of the Lambert Projection, we can continue to explore and understand the intricacies of our planet, fostering a deeper appreciation for its vast and complex beauty.




Closure
Thus, we hope this article has provided valuable insights into Unveiling the Power of the Lambert Conformal Conic Projection: A Comprehensive Guide. We appreciate your attention to our article. See you in our next article!
